Vehicular Combat

概述
KEO車輛格鬥 範例是一個以Quantum組建的車輛的格鬥遊戲。範例包含兩種類型的車輛(輕量越野車及重型8輪坦克),其用於在持續進行的自由殲滅戰中進行格鬥。
本範例由Redcatpig開發,並且是基於它們即將到來的遊戲KEO。
技術聚焦點
- 附有駕駛物理的車輛控制器
- 多重軸設置支援
- 動態懸吊檢視公式
- 損傷系統
- 即時命中判定武器系統
畫面截圖




下載
| 版本 | 發布日期 | 下載 | ||
|---|---|---|---|---|
| 2.1.0 | 2023年5月11日 | Quantum 車輛格鬥 2.1.0 組建 214 | ||
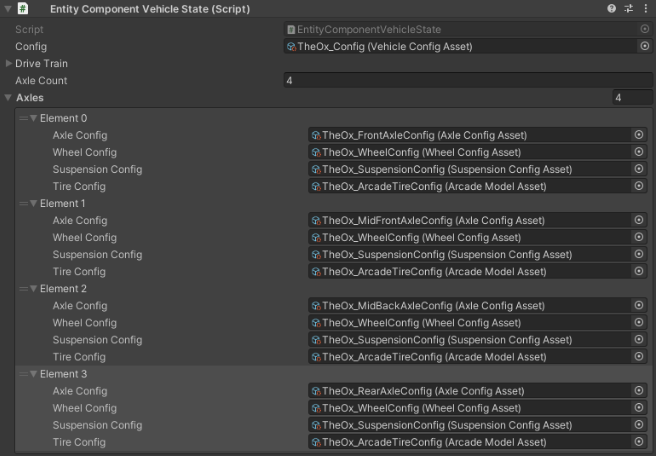
多重軸設置支援
範例預設支援最多4個輪軸及8個輪子(每個輪軸2個輪子)。透過增加VehicleState元件中的固定陣列大小,可以建立具有更多輪軸及輪子的車輛;只需將其設定為最大的車輛可以擁有的最大輪軸數量。
C#
component VehicleState {
asset_ref<VehicleConfig> Config;
DriveTrain DriveTrain;
Byte AxleCount;
array<AxleState>[4] Axles; // modify this value for support more axles
[HideInInspector] FP TimeFlipped;
[HideInInspector] FP TimeFalling;
[HideInInspector] FP Fuel;
}
輪軸設定
針對各個車輛,對於該特定車輛設定Axle Count。各個輪軸需要AxleConfig、WheelConfig、SuspensionConfig及TireConfig發揮功能。
輪軸設置
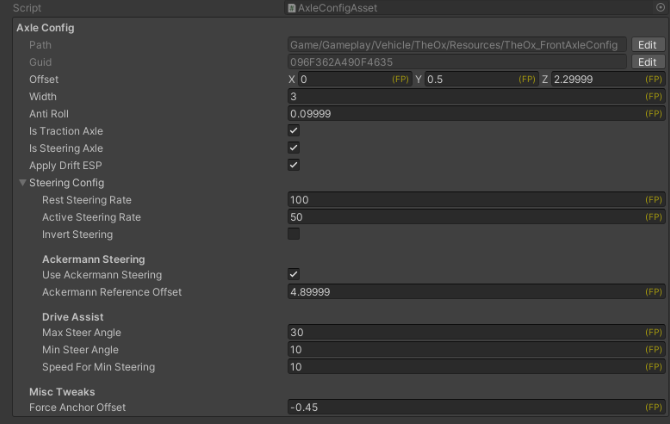
AxleConfig允許設定輪軸的偏移,其是對應於車輛的中心/樞軸的位置。
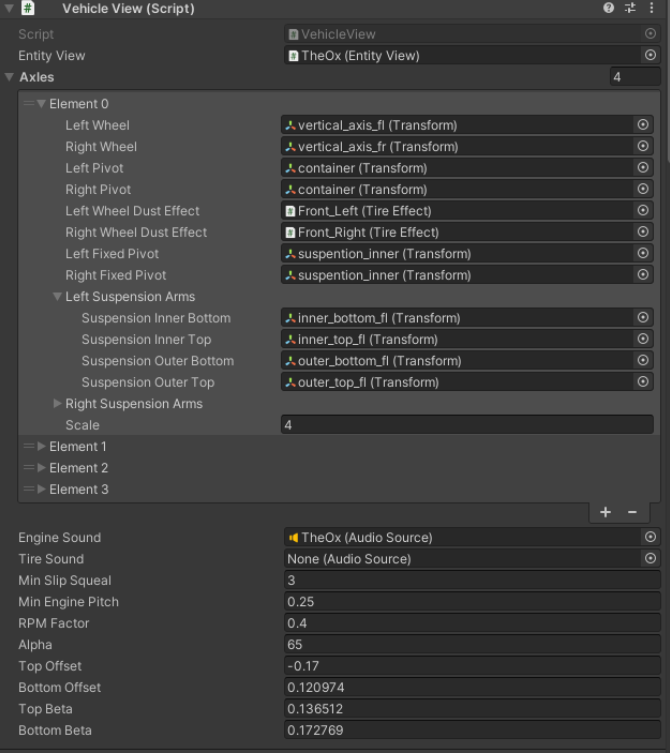
各個輪軸可以應用牽引力和/或轉向。如果輪軸位於車輛後部分,而且輪軸也應用轉向(比如在坦克車輛的情形),則必須檢查反向轉向選項,以讓輪子應用正確的轉向。
C#
struct AxleState {
asset_ref<AxleConfig> AxleConfig;
asset_ref<WheelConfig> WheelConfig;
asset_ref<SuspensionConfig> SuspensionConfig;
asset_ref<TireConfig> TireConfig;
[HideInInspector] FP SteerAngle;
[HideInInspector] WheelState WheelL;
[HideInInspector] WheelState WheelR;
}
駕駛輔助
在駕駛輔助章節,針對各個轉向輪軸的最大及最小轉向角度。這有助於玩家不會過度轉向或在更高的速度下失去控制。
懸吊
透過讀取Quantum模擬中的汽車物理的值,可以在Unity側上對懸吊進行視覺化。負責這個操作的類別稱為AxleView.cs。
由於這是純粹的視覺效果代表,懸吊視覺效果對模擬作出回應,但懸吊本身不屬於模擬的一部分。因此以下章節是完全關於Unity側代表及程式碼。
動態懸吊檢視
自訂懸吊檢視的範例中包含的公式,其特定用於KEO的車輛中建立的懸吊類型,但是該邏輯可以適用於其他懸吊類型。
懸吊由以下部分組成:
- 左/右輪子:視覺效果輪子,其將在其X軸上根據車輛的移動而旋轉。
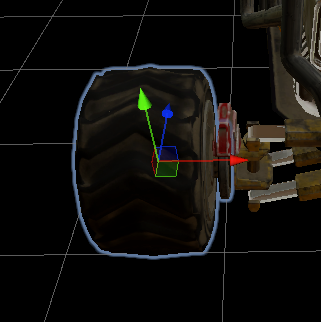
- 左/右樞軸:其物件將根據懸吊壓縮(取自Quantum模擬)來設定其Y位置,並且將在其Y軸上旋轉,以模擬轉向(輪子物件必須是樞軸的下層)。
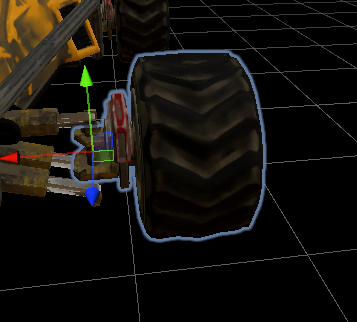
- 左/右固定樞軸:該物件將與輪子Y位置同步,並且包含懸吊桿的所有「內部」部件(在下方說明)。

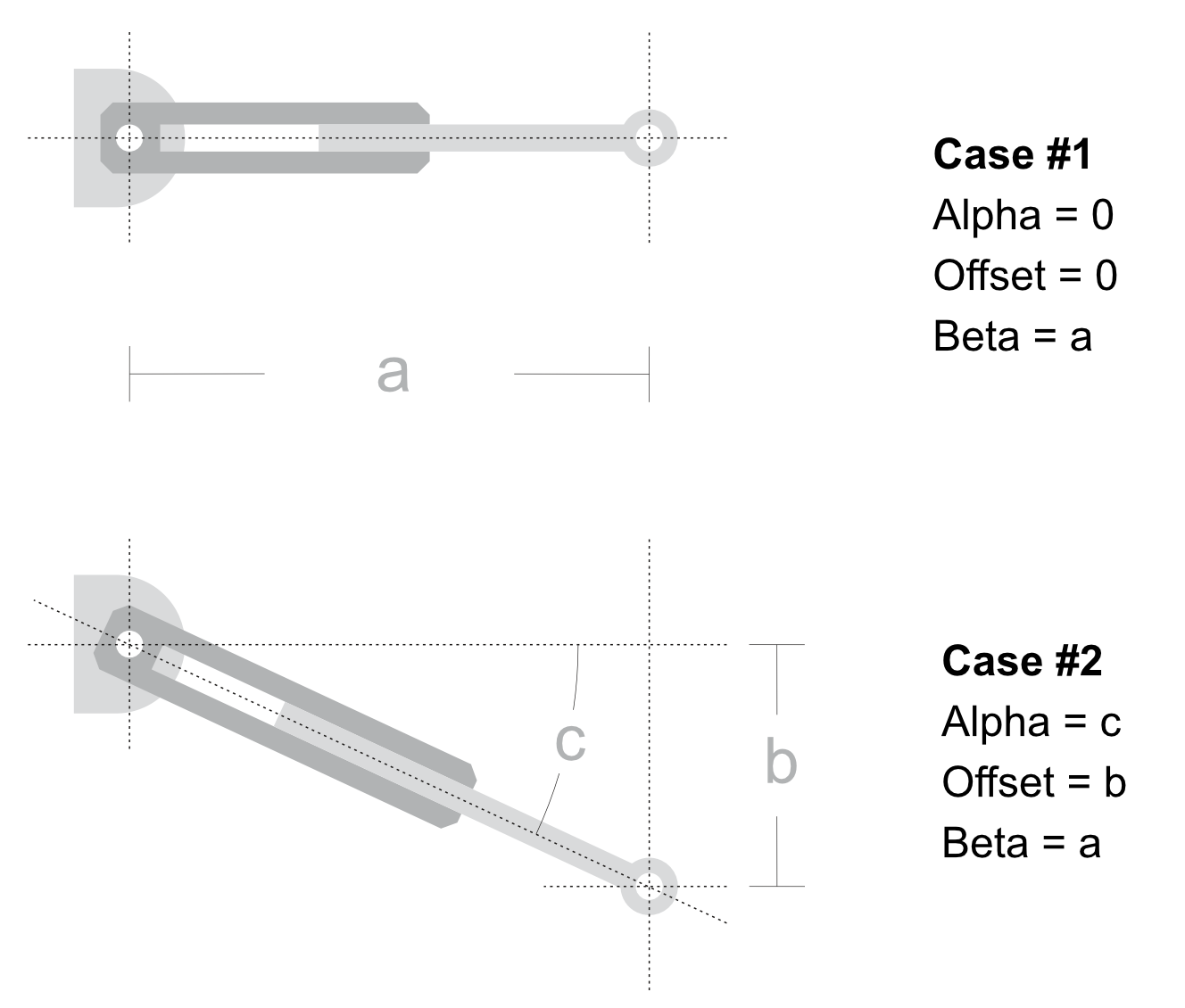
懸吊公式
懸吊桿由內部頂桿( A )、外部頂桿( B )、內部底( C )及外部底( D )所組成。

驅動視覺效果的公式如下:
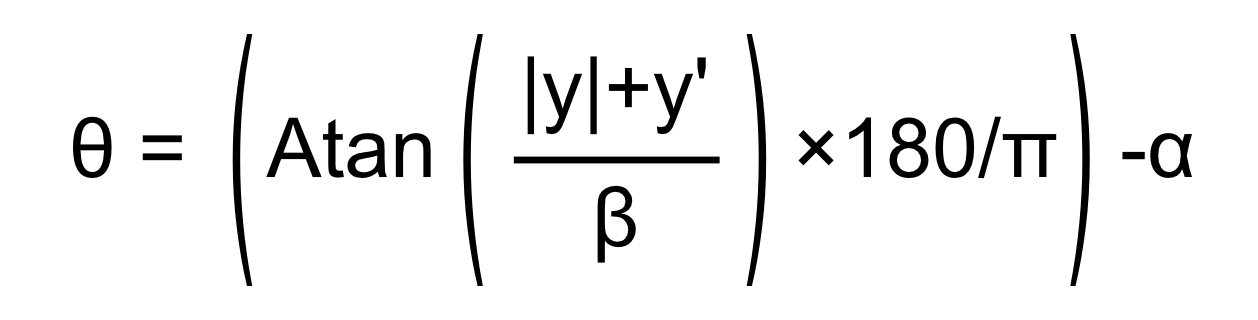
公式背後的概念是透過將輪子置於Y位置,並且相應地旋轉內部及外部懸吊部件,來模擬液壓桿的開啟與關閉。
為此,需要給定懸吊臂的起始角度(Alpha)。針對頂桿(案例 #1 ),起始角度總是為0,而針對底桿,則必須被測量(請參見在下方圖表中的案例 #2 中的Alpha)。也需要位移,也就是其與桿的旋轉位置的初始Y距離(請參見在下方圖表中的案例 #2 中的位移)。最後,必須考量在懸吊臂完全平行於世界的X軸時,懸吊臂的長度(Beta)(請參見案例 #1 中的Beta)。測量這些值的最好的方法是使用用於建立車輛的該3D軟體。
C#
LeftPivot.localRotation = Quaternion.Euler(0, axleState.WheelL.SteerAngle.AsFloat, 0);
RightPivot.localRotation = Quaternion.Euler(0, axleState.WheelR.SteerAngle.AsFloat, 0);
if (vehicleViewUpdateData.VehiclePhysicsBody->IsSleeping)
{
return;
}
// update wheels suspension travel
var suspensionMaxTravel = _suspensionConfig.MaxTravel.AsFloat;
var leftSuspensionCompression = axleState.WheelL.Suspension.CompressionPrevious.AsFloat - suspensionMaxTravel;
var rightSuspensionCompression = axleState.WheelR.Suspension.CompressionPrevious.AsFloat - suspensionMaxTravel;
LeftPivot.localPosition = _leftPivotPosition + new Vector3(0, leftSuspensionCompression + _anchorOffset, 0) / Scale;
RightPivot.localPosition = _rightPivotPosition + new Vector3(0, rightSuspensionCompression + _anchorOffset, 0) / Scale;
LeftFixedPivot.localPosition = _leftFixedPivotPosition + new Vector3(0, leftSuspensionCompression + _anchorOffset, 0) / Scale;
RightFixedPivot.localPosition = _rightFixedPivotPosition + new Vector3(0, rightSuspensionCompression + _anchorOffset, 0) / Scale;
C#
float angleTop;
float angleBottom;
if (wheelLocalPos.y < 0)
{
angleBottom = (Mathf.Atan((Mathf.Abs(wheelLocalPos.y) + _vehicleView.BottomOffset) / _vehicleView.BottomBeta) * 180 / Mathf.PI - _vehicleView.Alpha) * -1;
angleTop = (Mathf.Atan((Mathf.Abs(wheelLocalPos.y) + _vehicleView.TopOffset) / _vehicleView.TopBeta) * 180 / Mathf.PI) * -1;
}
else
{
angleBottom = Mathf.Atan((Mathf.Abs(wheelLocalPos.y) + _vehicleView.BottomOffset) / _vehicleView.BottomBeta) * 180 / Mathf.PI - _vehicleView.Alpha;
angleTop = Mathf.Atan((Mathf.Abs(wheelLocalPos.y) + _vehicleView.TopOffset) / _vehicleView.TopBeta) * 180 / Mathf.PI;
}
if (leftSide)
{
angleTop = angleTop < 0 ? Mathf.Abs(angleTop) : angleTop * -1;
angleBottom = angleBottom < 0 ? Mathf.Abs(angleBottom) : angleBottom * -1;
}
suspensionInnerBottom.localRotation = Quaternion.Euler(new Vector3(0, 0, angleBottom));
suspensionInnerTop.localRotation = Quaternion.Euler(new Vector3(0, 0, angleTop));
suspensionOuterBottom.localRotation = Quaternion.Euler(new Vector3(0, 0, angleBottom));
suspensionOuterTop.localRotation = Quaternion.Euler(new Vector3(0, 0, angleTop));